复杂算法详解
动态规划
Dynamic programing 简称 dp
是一种把原问题分解为相对简单的子问题的算法, 来求解复杂的算法.
动态规划问题的特征
- 动态规划问题一般都是求最值, 比如求最长公共子序列, 矩阵最小路径和, 最长递增序列, 最小编辑距离等等.
- 求动态规划问题的基本操作是穷举, 因为要求最值, 所以几乎大部分情况都是要穷举的.
- 三要素: 重叠子问题, 具备最优子结构, 无后效性.(只有具备这三个特征的问题, 才可以用 dp)
- 动态规划算法的根本目的是解决冗余, 用空间换时间.
- 动态规划最难的地方是 找状态转移方程.
重叠子问题
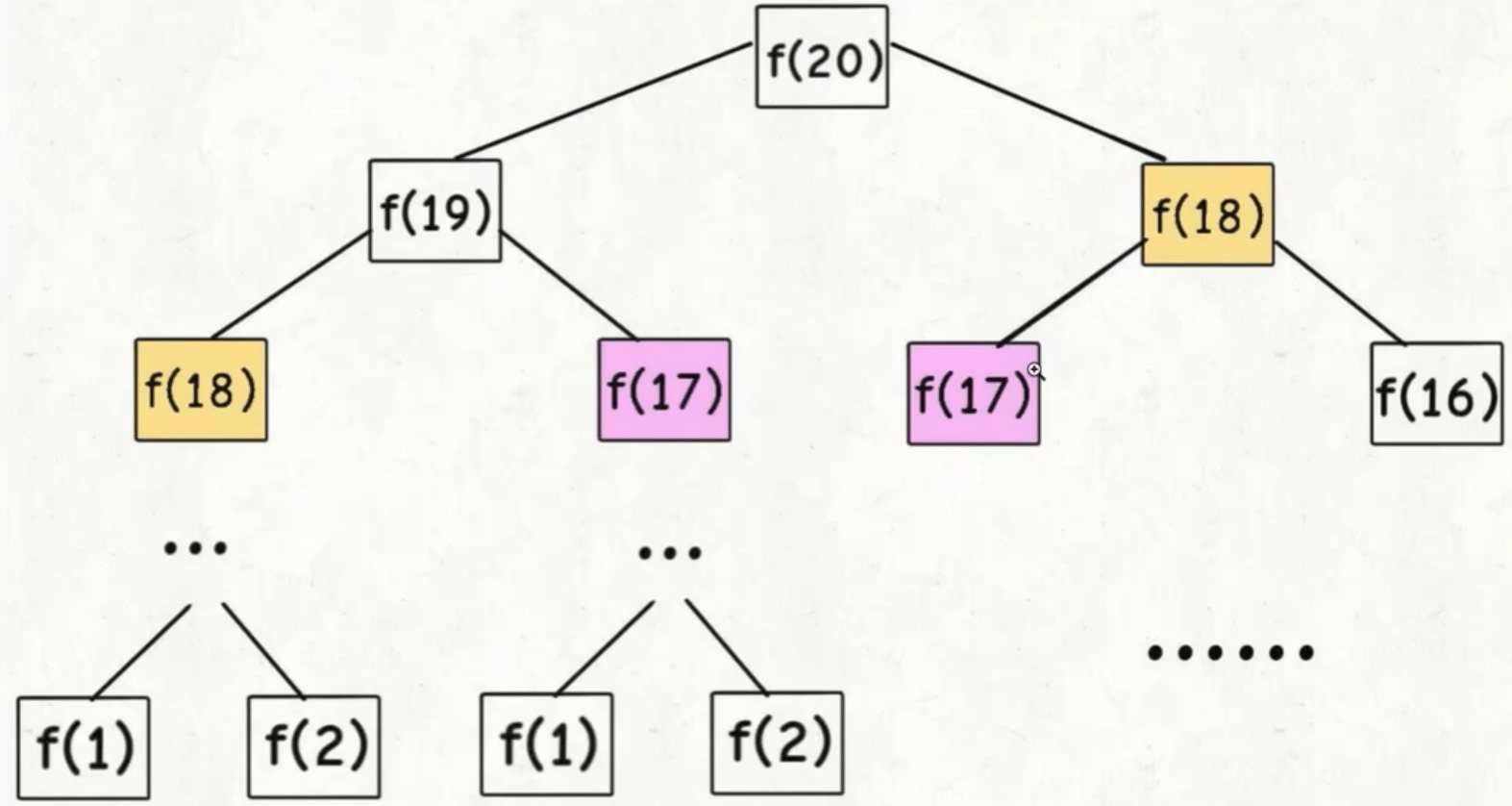
比如递归算法自顶向下对问题进行求解的时候, 每次产生的子问题并不总是新的问题, 可能某些子问题会被重复计算好多次.
dp 算法是利用了这种子问题的重叠性质, 对每个子问题呢, 值计算一次, 然后将其计算的结果保存在一个表格中.
当再次遇到这个子问题的时候呢, 我们就可以去表格中直接拿结果, 降低了时间复杂度.
最优子结构
如果问题结果的最优解, 所包含的子问题的解也是最优的, 并且每个子问题间相互独立, 那么就认为这个问题具备最优子结构.
无后效性
以前的状态和以前的状态转移方程, 不会影响将来的状态变化, 将来的状态只能由当前状态直接影响.
状态转移方程
比如高中学过的, 斐波那契数列.
0 1 1 2 3 5 8 13 21 34
F(n) 是指第几个位置的值.
递推公式: F(1) = 1, F(2) = 1, F(n) = F(n - 1) + F(n - 2)
n 的状态是由 n - 1 和 n - 2 的状态相加转移过来的.
当我们知道了 n - 1 阶段的状态和结果时, 我们可以通过某种对应关系来得到下一阶段 n 的状态.
解题思想
- 明确 base case
- 明确状态(理解为现在已知的变量)
- 明确选择(前一阶段如何转换为后一阶段)
- 定义 dp 数组的含义
dp[0][0] = 0;
for 状态1 in 状态1的所有值
for 状态2 in 状态2的所有值
dp[状态1][状态2] = 选择的结果重叠子问题举例 - 斐波那契数列
普通递归
function fib(n) {
if (n === 0) {
return 0;
}
if (n === 1 || n === 2) {
return 1;
}
return fib(n - 1) + fib(n - 2);
}这种写法非常的低效!!! 因为它进行了好多多余的计算.
备忘录
维护一个数组, 记录已经计算出的结果, 我们一般称之为备忘录.
function fib(n) {
if (n === 0) {
return 0;
}
// n 一般是从 1 开始的, 数组的索引是从 0 开始的, [0, 1 ...]
let memoArr = new Array(n + 1).fill(0);
return fibHelper(memoArr, n);
}
function fibHelper(memoArr, n) {
if (n === 0 || n === 1) {
return 1;
}
if (!memeArr[n]) {
memoArr[n] = fibHelper(memoArr, n - 1) + fibHelper(memoArr, n - 2);
}
return memoArr[n];
}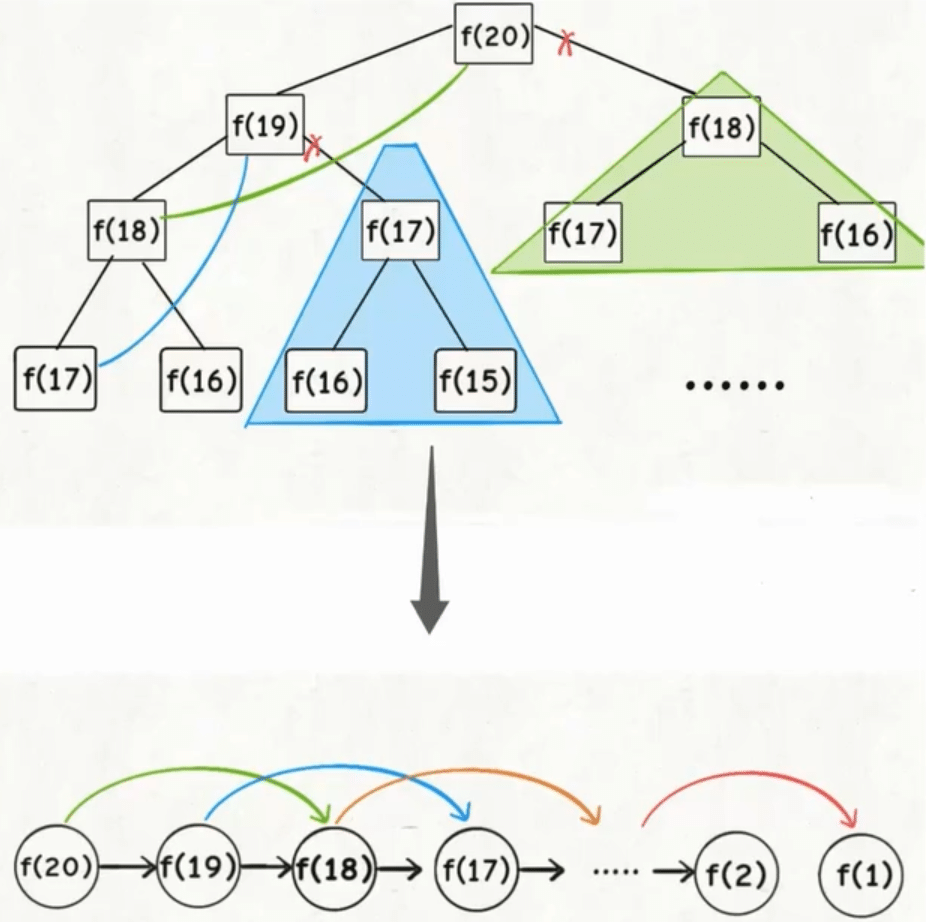
这种解法是自顶向下的查找并计算的, 直到 f(1) 和 f(2).
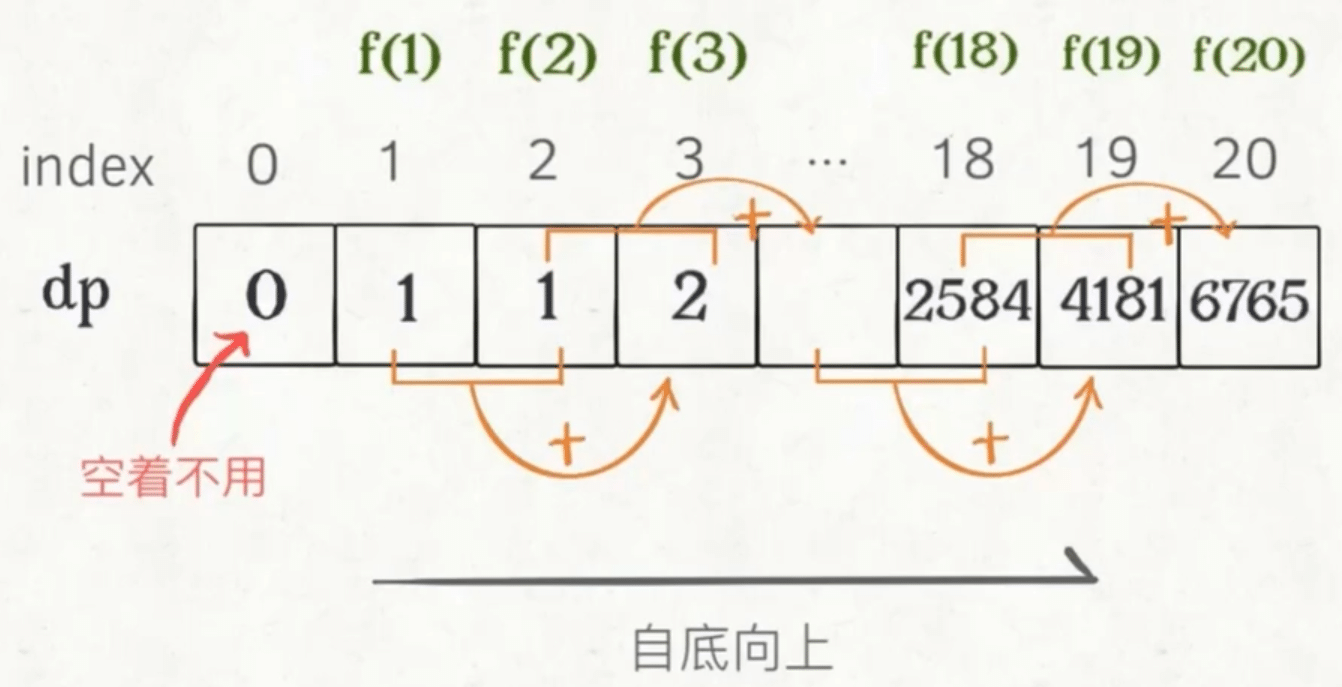
动态规划, dp 表的解法一般是自底向上的, 也就是从 f(1) 和 f(2) 开始推导, 直到 f(20).
dp
function fib(n) {
if (n === 0) {
return 0;
}
let dp = new Array(n + 1).fill(0);
dp[1] = 1;
dp[2] = 1;
for (let i = 3; i <= n; i++) {
dp[i] = dp[i - 1] + dp[i - 2];
}
return dp[n];
}
状态压缩
function fib(n) {
if (n === 0) {
return 0;
}
if (n === 1 || n === 2) {
return 1;
}
let prev = 1;
let current = 1;
for (let i = 3; i <= n; i++) {
const temp = prev + current;
prev = current;
current = temp;
}
return current;
}解题思路举例 - 零钱兑换问题
给定不同面额的硬币 coins, 和一个总金额 amount, 编写一个函数计算可以凑成总金额所需的最少硬币个数, 如果没有任何一种硬币组合能组成总金额, 返回 -1, 硬币数量无限.
coins = [1, 2, 5], amount = 11
结果应该输出 3(11 = 5 + 5 +1)
coins = [2], amount = 3
结果应该输出 -1
这是一个动态规划的问题, 因为它具备最优子结构.
比如想求 amount = 11 时的最少硬币数, 此时只需要知道 amount = 10 的最少硬币数.
确定 base case
dp[0] = 0; // dp[n] 代表凑出总金额为 n 所需要的硬币数
确定状态
状态就是原问题和子问题中会变化的量, 在此题中就是目标金额
coins, 硬币数量无限
唯一能变化的就是目标金额, 不断地向 base case 靠近
确定选择
选择是什么? 就是导致状态(目标金额)产生变化的行为
amount = 10
1 -> 9
2 -> 8
5 -> 5
明确 dp 数组的定义
一般呢 dp 数组的索引就是上面所提到的状态, dp 数组的每个值就是我们需要计算的数据
dp[i] 的定义: 当目标金额为 i 的时候, 至少需要 dp[i] 个硬币凑出
function coinChange(coins, amount) {
// 因为索引存在 0, 所以我们声明了 amount + 1 长度的数组
// 如果我们要凑出 amount 金额, 我们最多所需要的硬币数量是 amount
let dp = new Array(amount + 1).fill(amount + 1); // amount + 1 作为一个无效的值
dp[0] = 0;
for (let i = 0; i < dp.length; i++) {
for (let coin of coins) {
if (i - coin < 0) {
continue;
}
// 比如输入的是 [1, 2, 5], amount = 11
// 选择 1, dp[11] = 1 个面额为 1 的硬币 + 剩余需要凑出 dp[11 - 1] 面额的最优解
dp[i] = Math.min(dp[i], dp[i - coin] + 1);
}
}
return dp[amount] === amount + 1 ? -1 : dp[amount];
}实战 - 最长公共子序列
给定两个字符串 text1 和 text2, 返回这两个字符串的最长公共子序列的长度.
一个字符串的子序列是指这样一个新的字符串: 它是由原字符串在不改变字符的相对顺序的情况下删除某些字符(也可以不删除任何字符)后组成的新字符串.
例如, "ace" 是 "abcde" 的子序列, 但 "aec" 不是 "abcde" 的子序列. 两个字符串的「公共子序列」是这两个字符串所共同拥有的子序列.
若这两个字符串没有公共子序列, 则返回 0.
示例1
输入: text1 = "abcde", text2 = "ace"
输出: 3
解释: 最长公共子序列是 "ace", 它的长度为 3
示例2
输入: text1 = "abc", text2 = "abc"
输出: 3
解释: 最长公共子序列是 "abc", 它的长度为 3
示例3
输入: text1 = "abc", text2 = "def"
输出: 0
解释: 两个字符串没有公共子序列, 返回 0
开始
凑零钱是一维数组的动态规划
最长公共子序列, LCS, 典型的二维动态规划
思路
明确 dp 数组的含义
对于两个字符串 s1 和 s2, 我们一般会构造这样一个二维的 dp 表
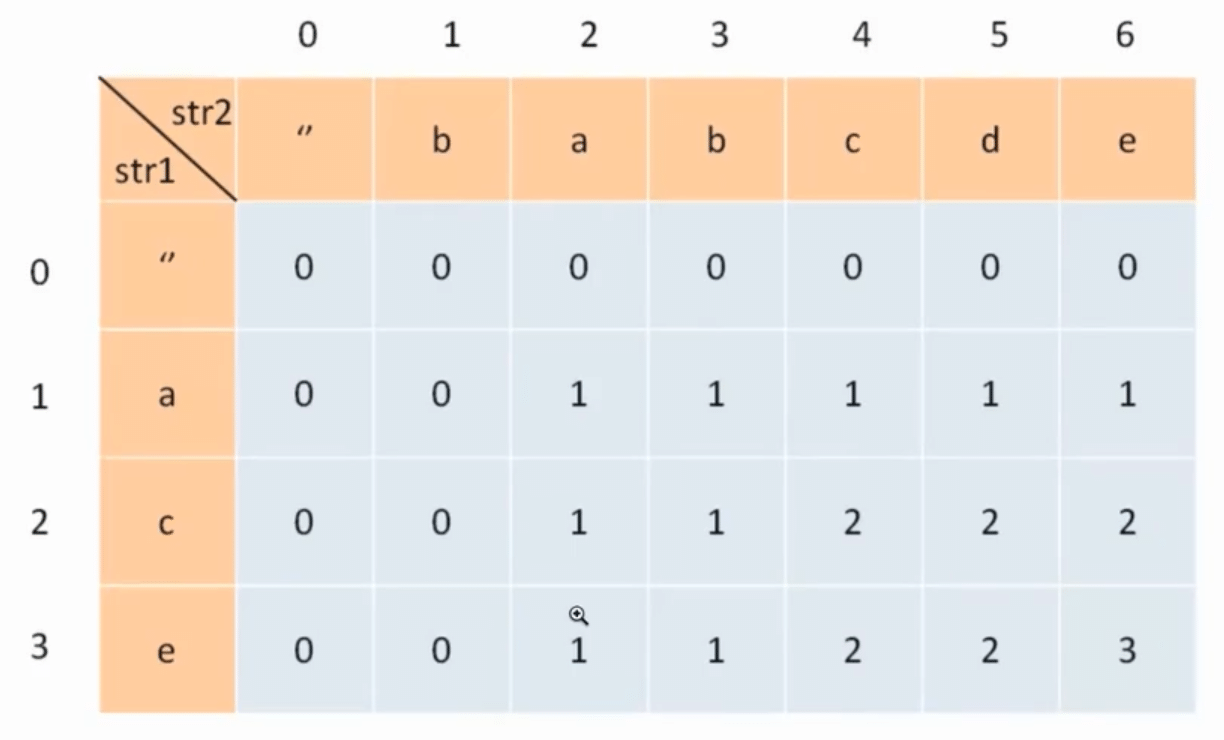
dp[i][j]的含义是, 对于 s1[1...i] 和 s2[1...j], 它们的 LCS 长度为dp[i][j].定义 base case
咱们表里用了索引为 0 的行和列表示空字符串, 也就是说
dp[0][j]和dp[i][0]都应该是 base case.比如
dp[0][3] = 0的含义是 ""和"bab"的 LCS 长度为 0.确定状态转移方程
对于 s1 和 s2 中的每个字符, 我们都有什么选择? 要么在 LCS 中, 要么不在
解题
如果某个字符存在于 LCS 中, 那么这个字符一定同时存在于 s1 和 s2
s1[i] === s2[j], 这个字符一定存在于 LCS, 此时 LCS 的长度 + 1, dp[i][j] = dp[i - 1][j - 1] + 1
s1[i] !== s2[j], 说明这两个字符里至少有一个不存在于 LCS 中, 我们需要从两个之中选择一个最大的. Math.max(dp[i][j - 1], dp[i - 1][j])
总结
/**
*
* @param {string} text1
* @param {string} text2
* @return {number}
*/
function longestCommonSubsequence(text1, text2) {
let n = text1.length;
let m = text2.length;
let dp = Array.from(new Array(n + 1), () => new Array(m + 1).fill(0));
for (let i = 1; i <= n; i++) {
for (let j = 1; j <= m; j++) {
if (text1[i - 1] === text2[j - 1]) {
dp[i][j] = dp[i - 1][j - 1] + 1;
} else {
dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
}
}
}
return dp[n][m];
}实战 - 最长回文子序列
我们对 dp 数组定义完后, 确定 base case 处于中间的对角线
dp[i][j] 需要从 dp[i + 1][j], dp[i][j - 1], dp[i + 1][j + 1] 转移而来.
我们最终要求的答案是 dp[0][n - 1]
这里看图一, 更清楚的弄明白题.
然后我们发现现在应该有两种正确的遍历方式, 这里再看图 2.
要么从左到右斜着遍历, 要么从下向上从左到右遍历, 这样才能保证每一步状态转移的过程中, dp[i][j] 的左边 下边 左下边都是经过计算过的.
// 给定一个字符串 s, 找到其中最长的回文子序列, 并返回该序列的长度. 可以假设 s 的最大长度为 1000.
// 示例 1:
// 输入:
// "bbbab"
// 输出:
// 4
// One possible longest palindromic subsequence is "bbbb".
// 示例 2:
// 输入:
// "cbbd"
// 输出:
// 2
// One possible longest palindromic subsequence is "bb".
// 链接:https://leetcode-cn.com/problems/longest-palindromic-subsequence
/**
* @param {string} s
* @param s
*/
function longestPalindromeSubseq(s) {
let length = s.length;
// dp[i][j] 表示的是从 s[i] 到 s[j] 之间的最长回文子序列的长度
let dp = Array.from(new Array(length), () => new Array(length).fill(0));
for (let i = length - 1; i >= 0; i--) {
// 每一个字符都是一个回文字符串, 因此对于 dp[i][i] 设置为 1
dp[i][i] = 1;
for (let j = i + 1; j <= length; j++) {
// 状态转移方程为:
// 当 s[i] 等于 s[j] 时, dp[i][j] = dp[i + 1][j - 1] + 2
// 当 s[i] 不等于 s[j] 时, dp[i][j] = max(dp[i - 1][j], dp[i][j + 1])
if (s[i] === s[j]) {
dp[i][j] = dp[i + 1][j - 1] + 2;
} else {
dp[i][j] = Math.max(dp[i + 1][j], dp[i][j - 1]);
}
}
}
return dp[0][length - 1];
}实战 - 编辑距离
我们对 dp 数组定义完后, 确定 base case 是 dp[x][0] 和 dp[0][y], 最终答案是 dp[x][y];
我们通过状态转移方程知道 dp[x][y] 需要从 dp[x - 1][y] 和 dp[x][y - 1] 转移而来.
那么根据上面两条特点, 我们很容易想到应该使用正向遍历
因为只有这样, 在每一步状态转移的过程中, 才能保证左边 上边 左上边的状态都是经过计算过的.
动态规划重点概念详解
最优子结构到底是什么?
"最优子结构"使某些问题的一种特定的性质, 而不只是动态规划特有的.
举例 最优子结构
比如学校有 10 个班, 现在已知每个班的最高成绩, 要求计算出全校的最高成绩.
是不是很简单, 直接在 10 个班的最高成绩中比较, 得出最大的即可.
这个问题就具有最优子结构, 每个班的最高成绩就是子问题, 子问题最优可以保证全局问题最优(但是这个问题不具有重叠子问题的特性, 所以没有必要用动态规划, 简单的比较一下就可以了)
举例 最优子结构 二叉树
求一棵二叉树的最大值
jsfunction maxVal(root) { if (root === null) { return -1; } const leftMax = maxVal(root.left); const rightMax = maxVal(root.right); return Math.max(root.val, leftMax, rightMax); }这个问题也是符合最优子结构的, 问题的答案可以通过子树的最大值推导出来
总结
- 最优子结构并不是动态规划独有的, 能求最值的问题大部分都具有这个性质
- 但是最优子结构使动态规划问题的必要条件
为什么动态规划遍历 dp 数组的方式五花八门, 有的正向遍历, 有的倒着遍历, 有的斜着遍历
同学们或许对 dp 数组的遍历顺序摸不着头脑
正向遍历
jslet dp = new Array(m).fill(new Array(n)); // m 行 n 列 for (let i = 0; i < m; i++) { for (let j = 0; j < n; j++) { // 计算具体的 dp[i][j] } }反向遍历
jsfor (let i = m - 1; i >= 0; i--) { for (let j = n - 1; j >= 0; j--) { // 计算具体的 dp[i][j] } }斜着遍历
jsfor (let l = 2; l <= n; l++) { for (let i = 0; i <= n - l; i++) { let j = l + i - 1; // 计算具体的 dp[i][j] } }
原则
如果你仔细观察的话, 会发现两个重点, 也可以说是原则
- 遍历过程中, 所需的状态必须是已经计算出来的
- 遍历的终点必须是存储结果的位置
总结一波
贪心算法
可以理解为是动态规划的一个特例, 贪心还需要满足一个特征"贪心选择性质"
- 贪心选择性质: 每一步做出的一个局部最优的选择, 最终的结果就是全局最优
斗地主 对手出了个 3
手上 3 4 5 6 7 8 9 2
区间调度问题
有很多[start, end] 的闭区间, 请设计一个算法, 算出这些区间中, 最多有几个互不相交的区间!
[8, 12] [9, 11] [13, 14]
贪心求解
我们是否可以每次都选择区间中开始最早的那个?
[0, 18] [1, 2] [2, 3] [3, 4]
我们是否可以都选择持续时间最短的?
[3, 6] [1, 3] [2, 4]
正确思路
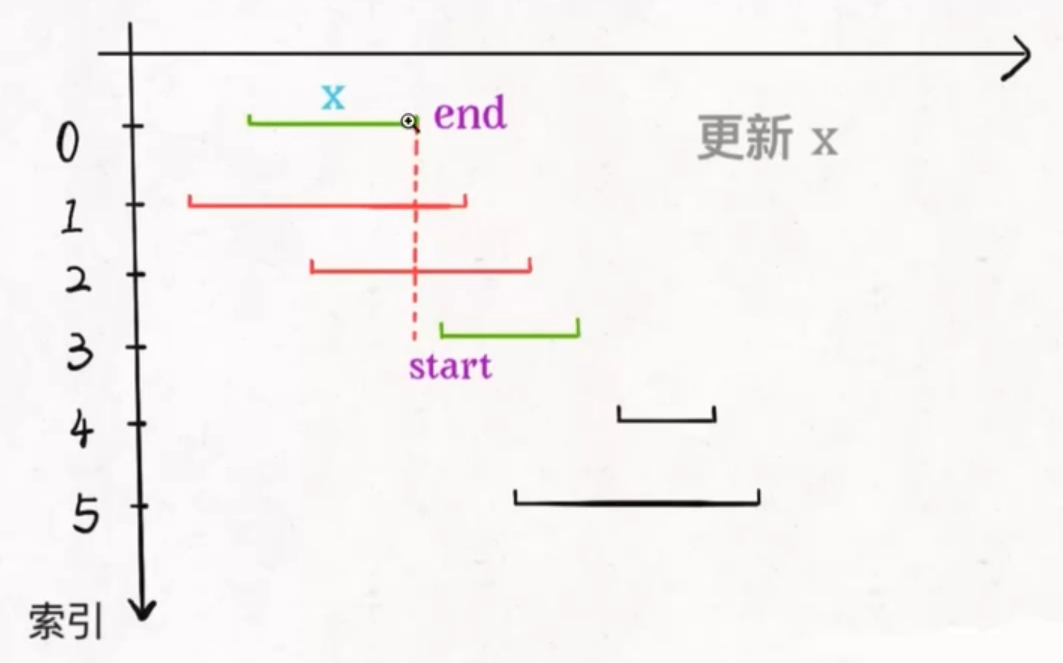
- 从可选的区间里, 选择一个结束 end 最小的区间 x
- 把所有和 x 相交的区间从 sum 中删除掉
- 重复 1 和 2 的循环, 之前选出的各种区间 x 就是我们所求的结果
/**
* 有许多[start, end]的闭区间, 请设计一个算法, 算出这些区间中, 最多有几个互不相交的区间.
* 比如 intvs = [[1, 3], [2, 4], [3, 6]]
* 这些区间最多有两个区间互不相交, 即 [1, 3] 和 [3, 6], intervalSchedule 函数此时应该返回 2.
* @param {Array<Array<number>>} intvs
* @return {number}
*/
function intervalSchedule(intvs) {
if (intvs.length === 0) {
return 0;
}
intvs.sort((a, b) => a[1] - b[1]); // 根据 end 升序排序
let xEnd = intvs[0][1];
let count = 1; // 互不相交的区间
for (const item of intvs) {
if (item[0] >= xEnd) {
count++;
xEnd = item[1];
}
}
return count;
}区间调度算法的应用
无重叠区间
给定一个区间的集合, 找到需要移除区间的最小数量, 使剩余区间互不重叠?
[1, 2] [2, 3] 不算做重叠
比如 输入 [[1, 2], [2, 3], [3, 4], [1, 3]]
输出 1
因为移除 [1, 3] 后, 剩下的区间互不重叠
jsfunction noOverlapInterval(intvs) { if (intvs.length === 0) { return 0; } intvs.sort((a, b) => a[1] - b[1]); // 根据 end 升序排序 let xEnd = intvs[0][1]; let count = 1; // 互不相交的区间 for (const item of intvs) { if (item[0] >= xEnd) { count++; xEnd = item[1]; } } return intvs.length - count; }用最少的箭头射爆气球
在二维空间中有好多气球, 气球的直径
[[10, 16], [2, 8], [1, 6], [7, 12]]
这个题的最终思想就是找出有几个互不相交的区间