Some Notes
Search K

Appearance

<

排序算法 ​

排序在解决什么问题 ​

  • 例如, 大学中的学生, 每个人都有自己的个人信息, 成绩等信息

    需要根据某一种信息, 以某种方式(升序/降序)重新排列这组数据

    姓名年龄班级评分
    张三20一班A
    李四21三班B

  • 以升序排列价格

    sort-taobao

  • 对字符串进行排序

    sort-baidu

  • 对文件夹进行排序

    sort-dir

排序 ​

问题: 需求具有相似性, 但是输入的数据格式完全不同. 有没有办法用同一种方式来解决重新排列的问题呢?

答案: 排序算法

问题: 排序算法如何处理全然不同的数据类型呢?

答案: 将比较的过程, 进行抽象. JavaScript 传入回调函数

sort-js

10 在 1 和 2 之间?

sort-js-comparator

手动传入 compare 回调后, 修复!

通过调用方传入比较方法, 将数据之间的比较与算法解耦, 使得算法能够处理任意的数据格式

全序关系 ​

全序关系即集合X上的反对称的、传递的和的二元关系(一般称其为≤).

若X满足全序关系, 则下列陈述对于X中的所有 a, b 和 c 成立:

  • 反对称性: 若 a ≤ b 且 b ≤ a, 则 a = b
  • 传递性: 若 a ≤ b 且 b ≤ c, 则 a ≤ c
  • 完全性: a ≤ b 或 b ≤ a

满足全序关系的集合叫做全序集合、线性序集合、简单序集合或链. 链还常用来描述偏序集合的全序子集.

全序关系的完全性可以如下这样描述: 集合中的任何一对元素都是可相互比较的.

注意完全性条件蕴含了自反性: a ≤ a, 因此全序关系也是(满足"完全性"条件的)偏序关系.

Compare 回调函数 ​

js
function compare(a, b) {
    return a - b;
}
  • 返回值 < 0, a < b
  • 返回值 > 0, a > b
  • 返回值 = 0, a = b

Date 与 compare ​

js
class Date {
    constructor(year, month, day) {
        this.year = year;
        this.month = month;
        this.day = day;
    }
    
    compareTo(other) {
        if (this.year < other.year) {
            return -1;
        }
        if (this.year > other.year) {
            return 1;
        }
        if (this.month < other.month) {
            return -1;
        }
        if (this.month > other.month) {
            return 1;
        }
        if (this.day < other.day) {
            return -1;
        }
        if (this.day > other.day) {
            return 1;
        }
        return 0;
    }
}

两个常用函数 ​

less(a, b)

当 a < b 时, 返回 true, 否则 false

js
function less(a, b) {
    return a - b < 0;
}

swap(a, i, j)

对数组 a, 在 i, j上的值进行交换

js
function swap(a, i, j) {
    const temp = a[i];
    a[i] = a[j];
    a[j] = temp;
}

选择排序 ​

基本思想 ​

遍历数组 a, 每次在当前的 index 上, 找到剩余数组中的最小值的索引, 为 min, 进行 swap a[index], a[min]

https://visualgo.net/zh/sorting

指针右移

js
i++

找到右边数组中的最小值

js
for (let j = i + 1; j < len; j++) {
    if (less(a[j], a[min])) {
        min = j;
    }
}
swap(a, i, min);

交换

js
swap(a, i, min);

结论 ​

js
function selectionSort(a) {
    const len = a.length;
    for (let i = 0; i < len - 1; i++) {
        let min = i;
        for (let j = i + 1; j < len; j++) {
            if (less(a[j], a[min])) {
                min = j;
            }
        }
        swap(a, i, min);
    }
}

复杂度分析 ​

选择排序, 一共经历 (N - 1) + (N - 2) + ... + 1 + 0 次 compare 和 N 次 swap.

(N - 1) + (N - 2) + ... + 1 + 0 ~ N2/2

O(N2)

结论: 时间主要消耗在 compare 上, swap 的用时可以忽略, 并且即使是已经排序完的数组需要花费同样的时间.

插入排序 ​

基本思想 ​

遍历数组 a, 在当前的 index 上, 向前比较, 如果顺序不对就进行交换

https://visualgo.net/zh/sorting

指针右移

js
i++

向左边的值查看顺序, 不符合则交换, 直到符合

js
for (let j = i; j > 0; j--) {
    if (less(a[j], a[j - 1])) {
        swap(a, j, j - 1);
    } else {
        break;
    }
}

结论 ​

js
function insertionSort(a) {
    const len = a.length;
    for (let i = 0; i < len; i++) {
        for (let j = i; j > 0; j--) {
            if (less(a[j], a[j - 1])) {
                swap(a, j, j - 1);
            } else {
                break;
            }
        }
    }
}

复杂度分析 ​

针对随机排序, 且无重复值的数组, 插入排序平均需要进行 ~ 1/4 N2 compare 和 ~ 1/4 N2 swap.

O(N2)

Best Case

已经排好序的数组, 进行插入排序

需要 N - 1 次 compare 和 0 次 swap

O(N)

Worst Case

数组排好序, 且逆序, 没有重复的值

插入排序需要 ~ 1/2 N2 次 compare 和 ~ 1/2 N2 次 swap

O(N2)

归并排序 ​

基本思想 ​

将数组分为两部分, 递归地, 对两个数组分别排序, 然后合并两个部分

https://visualgo.net/zh/sorting

归并

js
function _merge(a, aux, low, mid, high) {
    for (let k = low; k <= high; k++) {
        aux[k] = a[k];
    }
    let i = low, j = mid + 1;
    for (let k = low; k <= high; k++) {
        if (i > mid) {
            a[k] = aux[j++];
        } else if (j > high) {
            a[k] = aux[i++];
        } else if (less(aux[j], aux[i])) {
            a[k] = aux[j++];
        } else {
            a[k] = aux[i++];
        }
    }
}

结论 ​

js
function mergeSort(a) {
    /**
     * 分治
     * @param a
     * @param aux
     * @param low
     * @param high
     * @private
     */
    function _sort(a, aux, low, high) {
        if (high <= low) {
            return;
        }
        let mid = low + Math.floor((high - low) / 2);
        _sort(a, aux, low, mid);
        _sort(a, aux, mid + 1, high);
        _merge(a, aux, low, mid, high);
    }

    /**
     * 归并
     * @param a
     * @param aux
     * @param low
     * @param mid
     * @param high
     * @private
     */
    function _merge(a, aux, low, mid, high) {
        for (let k = low; k <= high; k++) {
            aux[k] = a[k];
        }
        let i = low, j = mid + 1;
        for (let k = low; k <= high; k++) {
            if (i > mid) {
                a[k] = aux[j++];
            } else if (j > high) {
                a[k] = aux[i++];
            } else if (less(aux[j], aux[i])) {
                a[k] = aux[j++];
            } else {
                a[k] = aux[i++];
            }
        }
    }

    const aux = a.slice();
    _sort(a, aux, 0, a.length - 1);
}

复杂度分析 ​

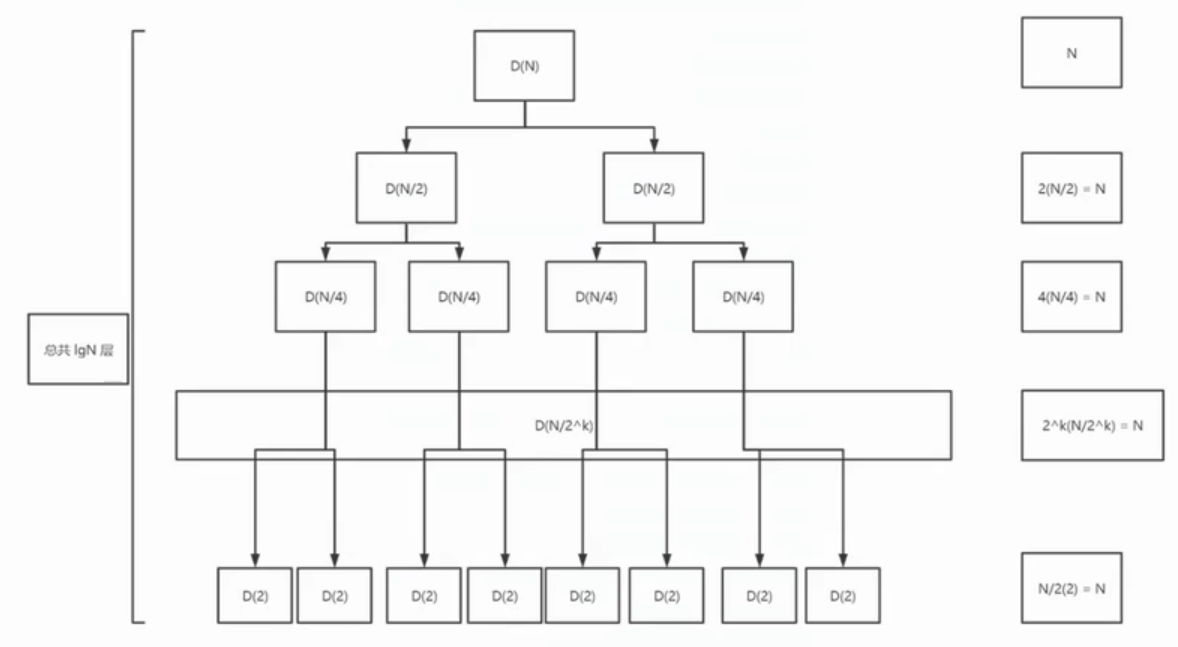
sort-merge

O(NlgN)

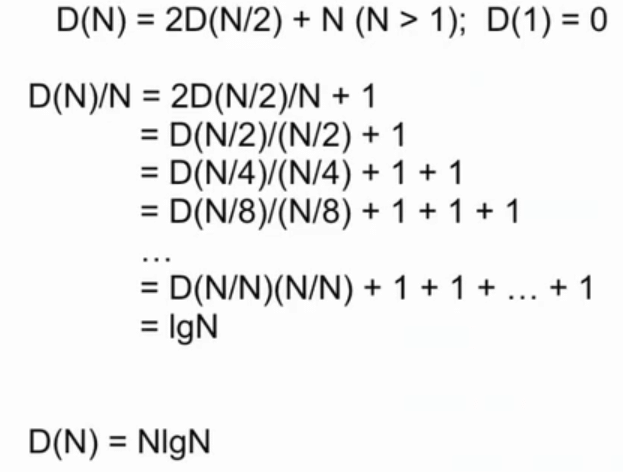
sort-merge-c

优化 ​

  1. 归并排序在当前数组长度较小时, 会分配很多小数组, 此时可以使用插入排序来替代小数组的排序.

    js
    const CUTOFF = 7;
function _sort(a, aux, low, high) {
    if (high <= low) {
        return;
    }
    if (high <= low + CUTOFF -1) {
        return insertionSort(a, low, high);
    }
    let mid = low + (high - low) / 2;
    _sort(a, aux, low, mid);
    _sort(a, aux, mid + 1, high);
    _merge(a, aux, low, mid, high);
}

  2. 对于已经排序好的数组, 则不需要再进行归并排序.

    排序后, 比较前半数组的最后一个值与后半数组的第一个值.

    js
    function _sort(a, aux, low, high) {
    if (high <= low) {
        return;
    }
    let mid = low + (high - low) / 2;
    _sort(a, aux, low, mid);
    _sort(a, aux, mid + 1, high);
    if (!less(a[mid + 1], a[mid])) {
        return;
    }
    _merge(a, aux, low, mid, high);
}

快速排序 ​

基本思想 ​

基于某个值 a[i], 对数组分区成两个部分

对各自的分区进行整理, a[i] 左边数组的所有值都小于等于 a[i], a[i] 右边数组的所有值都大于等于 a[i]

递归

对整理后的两个数组, 递归调用上述方法

https://visualgo.net/zh/sorting

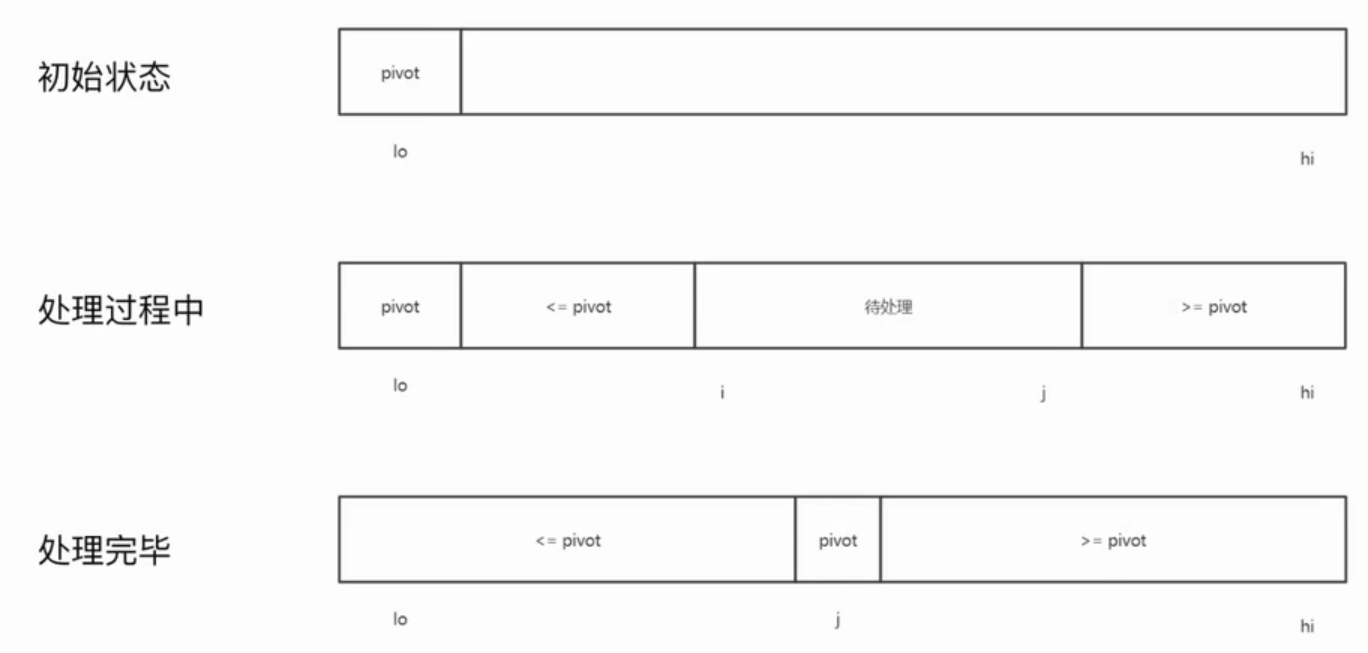
分区过程

重复下列过程, 直到 i 和 j 相交

从左向右找到下一个 i, 此时 a[i] ≥ a[lo]

从右向左找到下一个 j, 此时 a[j] ≤ a[lo]

交换 a[i], a[j]

最终, 交换 a[lo] 和 a[j]

sort-fast-partition

js
function partition(a, low, high) {
    let i = low;
    let j = high + 1;
    while(true) {
        while(less(a[++i], a[low])) {
            if (i == high) {
                break;
            }
        }
        while(less(a[low], a[--j])) {
            if (j == low) {
                break;
            }
        }
        if (i >= j) {
            break;
        }
        swap(a, i, j);
    }
    swap(a, low, j);
    return j;
}

确定 i

确定 j

处理完毕 跳出

交换 a[i] a[j]

交换 a[low] a[j]

结论 ​

js
function quickSort(a) {
    sort(a, 0, a.length - 1);

    /**
     * 排序
     * @param a
     * @param low
     * @param high
     */
    function sort(a, low, high) {
        if (high <= low) {
            return;
        }
        let j = partition(a, low, high);
        sort(a, low, j - 1);
        sort(a, j + 1, high);
    }

    /**
     * 分区
     * @param a
     * @param low
     * @param high
     * @returns {*}
     */
    function partition(a, low, high) {
        let i = low;
        let j = high + 1;
        while(true) {
            while(less(a[++i], a[low])) {
                if (i == high) {
                    break;
                }
            }
            while(less(a[low], a[--j])) {
                if (j == low) {
                    break;
                }
            }
            if (i >= j) {
                break;
            }
            swap(a, i, j);
        }
        swap(a, low, j);
        return j;
    }
}

有一些快速排序的实现, 生成额外的数组, 这样可以更容易实现分区, 不过没有必要.

快速排序不需要申请额外的空间.

复杂度分析 ​

对长度为 N 的数组, 且无重复的 key, 快速排序需要进行 ~2NlgN 的 compare, 和 ~1/3 NlgN 的交换.

Worst case

退化成冒泡排序, N + (N - 1) + (N - 2) + ... + 1 ~1/2 N2

最差情况从 NlgN -> N2

[^解决方案]: 可以对数组在排序进行 shuffle 的操作

优化 ​

  1. 在处理长度较小数组的时候, 使用插入排序替代.

    js
    const CUTOFF = 10;
function sort(a, low, high) {
    if (high <= low + CUTOFF - 1) {
        return;
    }
    let j = partition(a, low, high);
    sort(a, low, j - 1);
    sort(a, j + 1, high);
}

  2. 更换选择 pivot 的算法, 最好的情况就是选择到了中位数. 所以解决方案就是要尽量推断出中位数.

    随机选择 3 个值, 取其中位数.

    js
    function sort(a, low, high) {
    if (high <= low) {
        return;
    }
    const m = medianOf3(a, low, low + (high - low) / 2, high);
    swap(a, low, m);
    
    let j = partition(a, low, high);
    sort(a, low, j - 1);
    sort(a, j + 1, high);
}

稳定度 ​

快速排序是 非稳定排序

什么是稳定性

ij0123
B1C1C2A1
13B1C1C2A1
13B1A1C2C1
01A1B1C2C1

C1 C2 在排序后顺序转化成了 C2 C1

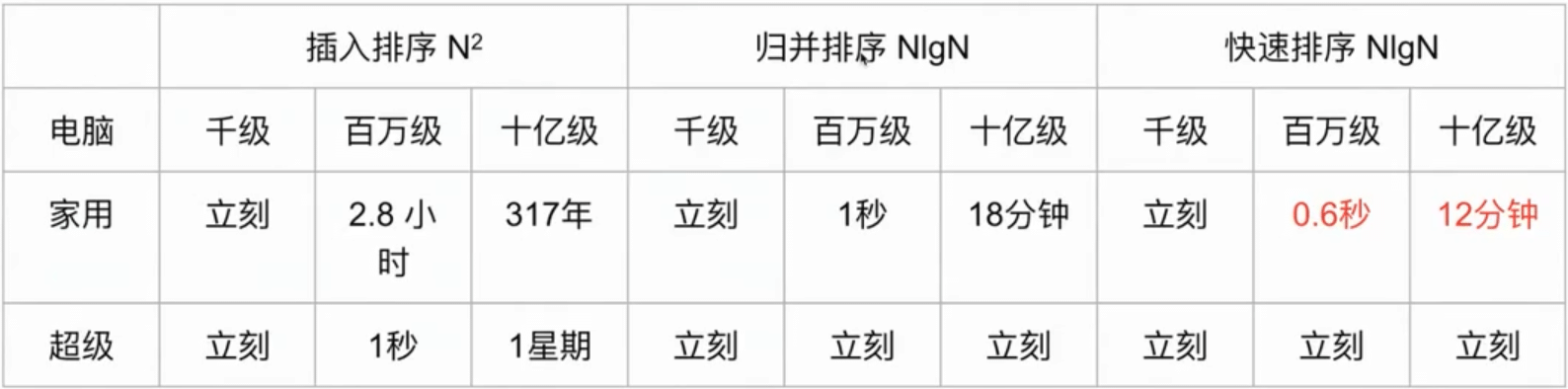
sort-pc

算法的复杂程度的减少, 远比电脑性能重要.

算法总结 ​

排序方法平均时间复杂度最坏时间复杂度空间复杂度稳定性
选择排序O(N2)O(N2)O(1)不稳定
插入排序O(N2)O(N2)O(1)稳定
归并排序O(NlgN)O(NlgN)O(N)稳定
快速排序O(NlgN)O(N2)O(1)不稳定